【Python】プログラムでフーリエ変換を理解しよう！【FFT, 標本化定理, ナイキスト周波数】

こんにちは。早く業務に慣れたい開発チーム入社１年目の髙垣です。

急ですが皆さん。ふと、音をフーリエ変換したい時ってありませんか？

ありますよね。

でも、「フーリエ変換って学校で計算式で習ったけど、結局は何をしているんだ？」となることありませんか？

そこで今回は計算式なんてほっといて、Pythonを使ってフーリエ変換が何をやっているのか体験してみましょう！

環境構築

下記リポジトリをクローンしてください

https://github.com/takaT6/fft-tutorial

クローンができたら下記のライブラリをインストールしてください↓

pip install numpy matplotlib japanize_matplotlib

japanize_matplotlib はmatplotlibに日本語を書き込めるようにするライブラリです。
日本語化をするにはフォントを入れたり、設定ファイルを変更したりする方法がありますが、japanize_matplotlibはimportするだけで適応されるのでおすすめです。

また、グラフの表示にmatplotlibを用いているので、GUI環境ではない方は plt.show()の部分をplt.savefig("sinwave.png") のように置き換えてファイルに出力してください。

おさらい：フーリエ変換とは

身近な音

普段、私たちが耳で聞いている"音"には室外機や車の音など様々な環境音が混ざっています。

そこで、"音"にどのような音が混ざっているかを解析する方法の1つが周波数解析で、それに使われる手法の1つがフーリエ変換です。

このフーリエ変換は信号を周波数解析するときに用いられ、地震波の解析、画像処理、音楽など身近なところで使われています。

ちなみに今回使うフーリエ変換は、離散フーリエ変換（DFT）を高速化させた高速フーリエ変換（FFT）を使います。

フーリエ変換と離散フーリエ変換

フーリエ変換と離散フーリエ変換は何が違うの？というと、フーリエ変換はアナログ信号に使用するのに対し、離散フーリエ変換はデジタル信号に使用します。

アナログ信号は連続的な信号で、デジタル信号は離散的な信号なので、それぞれ適した処理方法を用いるのです。

FFTとDFT

高速フーリエ変換（FFT）と離散フーリエ変換（DFT）の違いは処理速度です。

処理速度はもちろんFFTのほうが上で、詳細は割愛しますがDFTの計算量が\(O(N^{2})\)に対して、DFTを高速化したFFTの計算量は\(O(N\log_{2}{N})\)となり、FFTが大幅に高速です。

フーリエ変換は"変換"とつくように、時間領域の信号を周波数領域に変換します。

上の画像の青や赤、緑のグラフはX軸方向の単位は時間ですが、フーリエ変換するとX軸の単位が周波数に変わります。

つまり、緑のグラフをフーリエ変換しても、直接赤と青のグラフは得られないということです。

言葉で説明されてもあれなので、実際にプログラムを実行してフーリエ変換を体験してみましょう！

入力信号の作成

今回は簡単な例として2Hzと8Hzの正弦波を使って入力信号を作りたいと思います。

正弦波のプログラム

まず、核となる正弦波のy軸（振幅）とx軸（時間）を計算するプログラムです。

sinwave.py

import sys
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib

sf = 44100  # サンプリング周波数 [Hz]
sec = 1.0     # 信号の長さ [s]
dt = 1/sf   # サンプリング周期 [s]
A = 1.0     # 振幅
f = float(sys.argv[1])    # 周波数 [Hz]
t = np.arange(0, sec, dt) # サンプリング点の生成
y = A*np.sin(2*np.pi*f*t) # 正弦波の生成

plt.plot(t, y, color="b")
plt.xlabel('時間[s]', fontsize=10)
plt.ylabel('振幅', fontsize=10)
plt.show()

コード解説

・サンプリング周波数：1秒間に音を取得する回数。数値が高いほど滑らかな波形になります。音楽でいうと音質の部分です。44100回/秒（=Hz）に設定しています。
・サンプリング周期：サンプリングの間隔です。ササンプリング周波数を44100回/秒と設定しているので 1秒 / 44100回 ≒ 0.00002秒に1回サンプリングします。
・振幅：音の強さです。音楽でいうと音量です。
・周波数：１秒間に何回信号を繰り返すかです。ここでは引数で指定できます。音楽でいうと高音、低音です。

ちなみに441000Hzという数値はCDのサンプリング周波数でもあります。

t = np.arange(0, sec, dt) # サンプリング点の生成

ここでx軸のデータを生成していて、sec=1なので約0.00002秒間隔の44100個のデータを保持しています。

y = A*np.sin(2*np.pi*f*t) # 正弦波の生成

これは正弦波の公式を使って、上記のx軸のデータに対応するy軸のデータを生成しています。

実行

python sinwave.py 任意の周波数

正弦波の作成

このプログラムを使って、2Hzと8Hzの正弦波がどのような波形なのかチェックしましょう！

check_sinwaves.py

import numpy as np
import matplotlib.pyplot as plt 
import japanize_matplotlib

sf = 44100    # サンプリング周波数 [Hz]
sec = 1.0    # 信号の長さ [s]
dt = 1.0/sf   # サンプリング周期 [s]
A = 1.0      # 振幅
t = np.arange(0, sec, dt) # サンプリング点の生成

y2Hz = A*np.sin(2*np.pi*2.0*t) # 2Hzの正弦波の生成
y8Hz = A*np.sin(2*np.pi*8.0*t) # 8Hzの正弦波の生成

plt.plot(t, y2Hz, color="b") # y-tグラフのプロット
plt.plot(t, y8Hz, color="r") # y-tグラフのプロット
plt.xlabel('時間[s]', fontsize=10)
plt.ylabel('振幅', fontsize=10)
plt.show()

11,12行目で2Hzと8Hzの信号を作っています。

実行

python check_sinwaves.py

結果

実行して、下記のように表示されたらOKです！

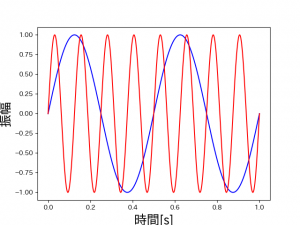
青線が2Hzの正弦波で、赤線が8Hzの正弦波です。

x軸は１秒間なので、画像からそれぞれ、1秒間に2回と8回の信号が含まれていることがわかります。

正弦波の合成

次に、この２つの信号を合成して入力信号を作りたいと思います。

使用するプログラムはこちらです↓

combine_sinwaves.py

import numpy as np
import matplotlib.pyplot as plt 
import japanize_matplotlib

sf = 44100    # サンプリング周波数 [Hz]
sec = 1.0    # 信号の長さ [s]
dt = 1.0/sf   # サンプリング周期 [s]
A = 1.0      # 振幅
t = np.arange(0, sec, dt) # サンプリング点の生成

y2Hz = A*np.sin(2*np.pi*2.0*t) # 2Hzの正弦波の生成
y8Hz = A*np.sin(2*np.pi*8.0*t) # 8Hzの正弦波の生成

y_combine = y2Hz + y8Hz # 2つを合成

plt.plot(t, y_combine, color="g")
plt.xlabel('時間[s]', fontsize=10)
plt.ylabel('振幅', fontsize=10)
plt.show()

実行

python combine_sinwaves.py

結果

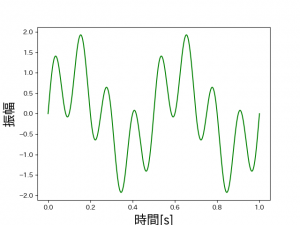
いい感じですね。

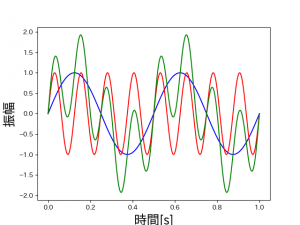
3つのグラフを並べると、8Hzの波形に2Hzがノイズとなり、波形が入り乱れています。

今回はこの緑線の信号を入力信号として使っていきます。

フーリエ変換をして波形を解析しよう

入力信号が作成できたので、フーリエ変換を使って周波数解析をしてみましょう！

今回使うフーリエ変換はnumpyに標準で備わっているnp.fft.fft()を使います。

fft.py

import numpy as np
import matplotlib.pyplot as plt 
import japanize_matplotlib

sf = 44100    # サンプリング周波数 [Hz]
sec = 1.0     # 信号の長さ [s]
dt = 1.0/sf   # サンプリング周期 [s]
A = 1.0       # 振幅
t = np.arange(0, sec, dt) # サンプリング点の生成

y2Hz = A*np.sin(2*np.pi*2.0*t) # 2Hzの正弦波の生成
y8Hz = A*np.sin(2*np.pi*8.0*t) # 8Hzの正弦波の生成

y_combine = y2Hz + y8Hz # 2つを合成

N = int(sf *sec) #データ点数

# 高速フーリエ変換
F = np.fft.fft(y_combine)

# 周波数軸
freq = np.fft.fftfreq(N, d=dt)

# 振幅スペクトル
Amp = np.abs(F / (N / 2))

plt.plot(freq[:10], Amp[:10])
plt.xlabel('周波数[Hz]', fontsize=10)
plt.ylabel('振幅スペクトル', fontsize=10)
plt.show()

コード解説

# 周波数軸
freq = np.fft.fftfreq(N, d=dt)

最初のfreq[0]は0Hzになっており、maxは44099Hzですが、標本化定理（サンプリング定理）により、サンプリング周波数の1/2の22050Hz以下でフーリエ変換の結果が有効となります。
また、サンプリング周波数の1/2のことをナイキスト周波数といいます。
ナイキスト周波数と標本化定理については後述します。

# 振幅スペクトル
Amp = np.abs(F / (N / 2))

ここでは振幅スペクトルを求めて元の信号の振幅に揃えています。
F/(N/2)を正規化すると言ったりします。

なぜこの処理が必要なのかは、データ点数NによってFFTで得られる振幅が変わってしまうからです。
今回は振幅をもとの信号と合わせたいため、正規化を行っています。
ちなみに正規化をしなくても、ピークが出る周波数は変わらないので、機器によっては正規化をあえて行わないものがあります。

plt.plot(freq[:10], Amp[:10])

理論上は22050Hzまで解析できるのですが、今回は2Hzと8Hzの信号しか含まれていないので、9Hzまでの表示にしています。

実行

python fft.py

結果

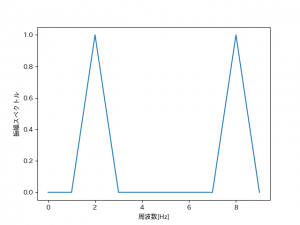
いい感じですね。

しっかりと2Hzと8Hzのところでピークが出ています。
振幅スペクトルも今回は振幅A=1で固定していたので両方とも強度が１になっています。

ちなみに8Hzの振幅A=4に変えてFFTを行うと、8Hzの振幅スペクトルが４に変化します。

y8Hz = 4*np.sin(2*np.pi*8.0*t) # 8Hzの正弦波の生成

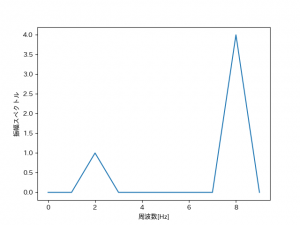
このようにFFTをすれば、音に含まれる周波数を解析して、どんな音が含まれているか解析することができます。

また、これを応用して高い周波数のみを除去するローパスフィルタや、その逆に低い周波数のみを除去するハイパスフィルタを用いてノイズ除去をしてクリーンな音を生成することもできます。

ナイキスト周波数と標本化定理について

フーリエ変換でまあまあ大切な概念がナイキスト周波数です。

このナイキスト周波数を理解するのに必要な原理が標本化定理、またの名をサンプリング定理といいます。

標本化定理をざっくり説明すると、「元の信号をその最大の周波数の２倍を超えた周波数で標本化（サンプリング）すれば、理論上は完全な波形を再現することができる」というものです。

例えば、元の信号が10Hzであれば、サンプリング周波数を20Hzより高くすれば、再び10Hzの信号に戻せるというわけです。
逆に言えば、サンプリング周波数の半分未満の周波数信号なら再現可能ということです。

そして、このサンプリング周波数の半分の周波数のことをナイキスト周波数といいます。

下記の図のように、2Hzの信号をだんだんとサンプリング周波数を落としてサンプリングしていくと、元の信号の情報が失われていきます。
サンプリング周波数を小さくしていった結果、最終的に元の信号が再現できなくなる境界線がナイキスト周波数ということです。

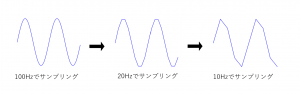
つまり、このナイキスト周波数を考慮すると、FFTで解析できる周波数は理論上はナイキスト周波数までということになります。
もし、ナイキスト周波数よりも高い周波数が含まれていた場合、折り返し歪み（エイリアシング）が発生してしまい元の信号を復元できなくなります。

折り返し歪み（エイリアシング）の原理を簡単に解説すると、ナイキスト周波数が50Hz（サンプリング周波数が100Hz）でサンプリング前の信号が70Hzの場合、70Hzの信号はナイキスト周波数で折り返し、30Hzに見えます。

実際に折り返し歪み（エイリアシング）が発生しているかを確認するためfft.pyを下記のように変更しましょう。

sf = 100    # サンプリング周波数 [Hz]

# y2Hz = A*np.sin(2*np.pi*20.0*t) # 2Hzの正弦波の生成
# y8Hz = A*np.sin(2*np.pi*70.0*t) # 8Hzの正弦波の生成

y20Hz = A*np.sin(2*np.pi*20.0*t) # 20Hzの正弦波の生成
y70Hz = A*np.sin(2*np.pi*70.0*t) # 70Hzの正弦波の生成

y_combine = y20Hz + y70Hz # 2つを合成

上記のコードでは20Hzと70Hzの信号を合成しています。

plt.plot(freq[:50], Amp[:50])

結果

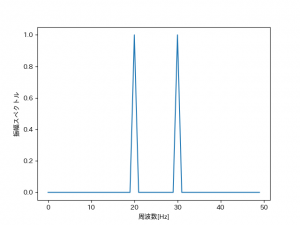
「20Hzと70Hz」にピークが立つべきところが、70Hzの信号はナイキスト周波数で折り返され、50-20=30Hzでピークが現れています。

このように、フーリエ変換をするときはナイキスト周波数以上の周波数が含まれていないかどうかに注意する必要があります。

まとめ

今回はフーリエ変換の仕組みをPythonのプログラムを用いて解説しました。

RaccoonTechBlogでは異質のマニアックな内容になってしまいましたが、この記事でフーリエ変換の挙動を理解していただけたら幸いです。

最後になりましたが、ラクーングループは一緒に働く仲間を絶賛大募集中です！
原理を知ることの大切さをとても推奨される会社です。弊社のつよつよなエンジニア達に様々な助言をもらいながらエンジニアとして腕を磨きませんか？
ご興味を持っていただけましたら、こちらからエントリーお待ちしています！